Graphing with LiveCode, Part 2: Graphing Functions

I did a search for other ways to do graphing with LiveCode. I quickly found a tutorial on the RunRev site: http://lessons.runrev.com/s/lessons/m/4071/l/7049-how-to-make-a-simple-line-graph

This is worth a look as it provides a clever way to create static line graphs based on a list of numbers in a field. However, it doesn't seem to create a running, dynamic line graph of the kind I am trying to show in this series of blog postings.

Also, there is also a commercial product called ChartMaker for LiveCode:
http://www.flexiblelearning.com/chartmaker/

This is a LiveCode extension, meaning that you can extend the functionality of LiveCode to include making charts. It isn't too expensive (about $76), but then again, it isn't free. I don't know anything about it other than what I've read on the company's Web site. But, my cursory review of the product doesn't lead me to believe it can create dynmanic graphs "on the fly" either.

So, I think we still need to learn how to do this on our own with scripting in LiveCode.

In my last post, we learned how to "connect the dots" by using the brush tool (a bitmap graphic tool), choosing a brush color and shape, then dragging the brush from point to point using x,y coordinates where x and y are 0 at the top left corner of the LiveCode window. Now we need to learn how to use these skills to graph functions where y depends on x. I think the simplest example is y=x, meaning that whatever x is, y will be the exactly the same. So, the pairs of coordinates would be the following:

0,0

1,1

2,2

3,3

4,4

And so on...

So, how do we program LiveCode to graph y=x? It's easy. Here's the script for a button "Graph Function":

on mouseUp
   choose brush tool
   set the brush to 32
   set the brushColor to orange -- could use an RGB triplet here
   set the dragSpeed to 0
   //Set the starting point for the x and y variables:
   put 0 into var_x
   put 0 into var_y
   put 0 into var_xprev
   put 0 into var_yprev
  
   repeat 250 times
      //add one to var_x:
      put var_x+1 into var_x
      //This is the function "y=x" scripted in LiveCode:
      put 3*var_x+50 into var_y     
      drag from var_xprev, var_yprev to var_x, var_y
      put var_x into var_xprev
      put var_y into var_yprev
   end repeat
   choose browse tool
end mouseUp

And here is the resulting "graph," a line that is draw starting from the top-left corner of the window down to the center of the window (I set the window size of the stack to 500 x 500):

Let's now analyze and explain this script. First, many of you who received an "A" in algebra many years ago are probably saying "But shouldn't the graph be drawn going up and towards the right?" Yes, that is why you got an "A"! We will deal with this little problem before this post ends. Just try to ignore this problem for now.

Lines 7 and 8 set the two x and y variables both to 0. (I've kept with good scripting conventions and labeled them var_x and var_y to make it clear in the script that they are variables.) These lines set the starting point for the graph.

As we consider lines 9 and 10, you need to remember how the drag function works in LiveCode. You have to drag between two points. And, remember from my previous post that to draw a graph, we had to make sure that the ending point of one line segment became the starting point for the next line segment (i.e. connecting the dots). So, lines 9 and 10 set up two other variables that will be used to keep track of the coordinates of the end point of the previous line segment. Jump down to lines 18 and 19. These two lines pass the contents of var_x and var_y to these two variables I've cleverly named var_xprev and var_yprev (where 'prev' is short for previous). So, lines 9 and 10 just set these two variables also to 0 so that we have two pairs of numbers for the very first line segment. But, let's not get ahead of ourselves.

Lines 12 to 20 comprise a repeating loop that repeats 250 times. (In later posts, we'll get more sophisticated in how long or how far to graph. However, another good option -- if you want to be daring -- is to change line 12 to "repeat until the mouseClick" which will repeat forever until the mouse is clicked.)

Line 14 adds one to var_x, or 1+0, making it equal to 1. This is the classic way of incrementing a variable in a repeating loop.

Line 16, believe it or not, is the way we script the function "y=x" in LiveCode:

put var_x into var_y

In other words, putting x into y is the same as saying make y equal to x. So, var_y and var_x are both now 1.

Line 17 drags the brush between the two points. So, this script actually draws 250 individual line segments. (If you wanted to speed things up, you could change line 14 to "put var_x+2 into var_x" and repeat the loop only 125 times.)

As already mentioned, lines 18 and 19 pass the contents of var_x and var_y to var_xprev and var_yprev.

In algebra textbooks, you will see this function written in what is called the slope-intercept form:

y=mx+b

where m is the slope of the line and b is the place where the line intersects the y axis (known as the y-intercept). So, I know you are saying, "Cool! Let's do some stuff by including m and b in our equation!" (Man, you are geeky.)

OK, let's change line 16 to the following:

put 3*var_x+50 into var_y

Let's also change the brush color to orange in line 4, so the new line is easier to distinguish from the first line. Here is what we get when we run the script by clicking on the button:

As you can tell, the line is much steeper. That's because the slope is now 3. Also notice how the line starts down 50 pixels. Also notice that something a little weird happens right at the start. That weirdness is caused by the fact that var_x and var_y are still starting at 0 because of lines 7 and 8. Actually, when x is 0, y should 50 because 3x will equal 0. So, this is another little problem we need to solve. We can easily solve it by first setting var_xprev and var_yprev to some number far off to the top left, such as -1000, -1000. Do that and the graph now looks fine:

The computer has drawn an orange line from -1000,-1000 to 0,50, but we just can't see it because it is off to the left of the current window.

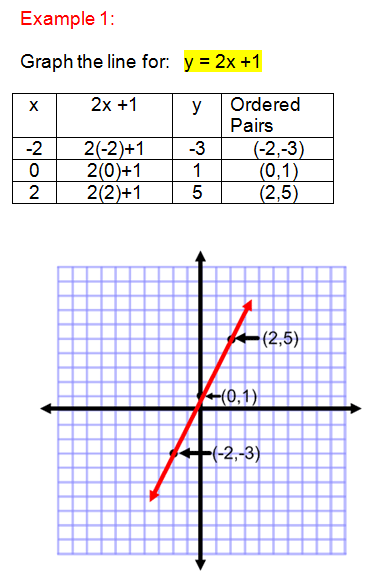
Let's draw one more line, using the function "y=2x+1". We need to update line 16 to the following:

      put 2*var_x+1 into var_y

I'll change the brush color to red. Here is the resulting graph:

I used this example because so we could compare it to what we would see in an algebra textbook. Here is a nice figure of the graph of y=2x+1 from http://www.algebra-class.com/table-of-values.html:

Two things jump out at me. First, their red line slants upward from left to right, not downward. Second, the 0,0 origin is at the center of the graph (not the top-left point). The first is a problem that results from the fact that in LiveCode the y axis simply goes in the other direction of the traditional Cartesian coordinate system. That problem will be easily solved just by multiplying all y values by -1. This will essentially "flip" the y axis.

To deal with the second issue, we need to choose 250,250 (the center of the window) as our starting point, instead of 0,0. So, we need to offset both x and y by 250 pixels.

OK, let's see how to do this. Let's start by graphing our original function of y=x. So, to flip the y axis, here is the script for line 16:

      put -(var_x) into var_y

This just means to put the negative of whatever var_x is into var_y.

Lines 17-19 have to be modified to add 250 to var_x and var_y, because of the offset:

      drag from var_xprev, var_yprev to var_x+250, var_y+250
      put var_x+250 into var_xprev
      put var_y+250 into var_yprev

Make these two changes and here is the resulting graph (I also changed the brush color back to brown):

Let's now enter our second function from above, making sure again to multiple var_x by -1. This changes line 16 to:

      put -(3*var_x+50) into var_y

Here's the resulting graph (I changed the brush color to orange to show the second line):

Perfect!

Let's end this rather long blog posting by using LiveCode's vector tools to draw the x and y axes, making sure that they cross exactly at point 250,250 (also be sure to draw these axis lines with arrows at both ends, otherwise your algebra teacher will find and reprimand you; the option to add arrow heads can be found in the "basic properties" window of each line). Here is a resulting graph that any algebra teacher would be proud of:

Note, something very important and wonderful. You can now change the origin of the graph just by manipulating these two numbers (currently 250). So, if you wanted the graph's origin to be over 100 and down 300, you would change these numbers accordingly.

In the next posting, we'll continue this graphing exploration by graphing the function for a parabola and the sine and cosine functions. I also promise in my next post to provide a LiveCode stack you can download with all of the scripts we've covered.