As promised, here is a copy of the LiveCode stack with all of the scripts from this and the previous two blog postings, along with Mac and Windows executable versions of each (for those of you who have not yet downloaded LiveCode, which would be strange given that it is now free):
Note: I just learned that when saving a stack that uses the brush tool as a stand-alone application, you have to go to the standalone settings, and under "General" choose to "select inclusions for the standalone application," then check "brushes."
Graphing Parabolas
Let's start with the parabola, which is derived from the function: y=x2
(This is read as "y equals x squared.")
Here are x, y pairs of numbers for this function:
-3,9
-2,4
-1,1
0,0
1,1
2,4
3,9
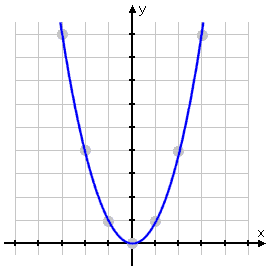
Here is a graph of a parabola linked from purplemath.com:
I just love how the curve mirrors itself around the y-axis due to the fact that a negative times a negative gives a positive.
Graphing a Parabola in LiveCode
Let's turn now to doing this in LiveCode. In the previous blog post, we ended with the script for a button that graphed a line of the following function:y=3x+50
Here's the entire script of that button:
on mouseUp
choose brush tool
set the brush to 32
set the brushColor to orange -- could use an RGB triplet here
set the dragSpeed to 0
//Set the starting point for the x and y variables:
put 0 into var_x
put 0 into var_y
put -1000 into var_xprev
put -1000 into var_yprev
repeat 250 times
//add one to var_x:
put var_x+1 into var_x
//This is the function "y=3x+50" scripted in LiveCode:
put -(3*var_x+50) into var_y
drag from var_xprev, var_yprev to var_x+250, var_y+250
put var_x+250 into var_xprev
put var_y+250 into var_yprev
end repeat
choose browse tool
end mouseUp
Line 5 of the repeat script is the LiveCode version of that function:
put -(3*var_x+50) into var_y
Recall that in order to "flip" the y-axis of LiveCode to match that of a traditional Cartesian coordinate system, we took the negative of the function, hence the negative sign near the beginning of the line. Also recall that we wanted the origin of the graph -- 0, 0 in a Cartesian system -- to be at the center of our 500 by 500 pixel large card. So, lines 6-8 add 250 to varx and vary to accomplish this. We repeated the loop 250 times because that seemed about right. (Don't you just love my precise way of describing things.)
Now we need to rewrite line 5 to graph not the function of the line "y=3x+50," but instead the function of the parabola "y=x2." A digital piece of cake.
put -(var_x^2) into var_y
Here is what the resulting graph looks like:
To flatten the curve out, we just need to divide y by some amount. In playing around, 50 worked out pretty well. There are a couple of ways to do this, but I think the simplest is just to change line 5 in the repeat loop to the following:
put -(var_x^2)/50 into var_y
When you run the script now, you only get a small arc graphed because we need to repeat the loop many more times. So, since we are dividing y by 50, we can calculate the largest x value by taking the square root of 250*50, which is not quite 112. So, let's repeat this loop 112 times and see what we now get:
Anyhow, play around with dividing y by 60 or 40 or 106, whatever, to see how to make the curve flatter or skinnier.
To get the full parabola (left and right halves), we just need to set the first value of x to the negative of the number of loops we needed to attain the perfect right half, then of course we need to double the number of times we repeat the loop.
Line 7 of the mouseUp script becomes:
put -112 into var_x
We will repeat the loop 224 times to get the following:
Here is the final script of my button "Graph y=x^2":
on mouseUp
choose brush tool
set the brush to 32
set the brushColor to brown -- could use an RGB triplet here
set the dragSpeed to 0
//Set the starting point for the x and y variables:
put -112 into var_x
put 0 into var_y
put -1000 into var_xprev
put -1000 into var_yprev
repeat 224 times
//This is the function "y=x squared" scripted in LiveCode:
put -(var_x^2)/50 into var_y
//put var_x&", "&var_y into line 1 of field "data"
//put var_x+250&", "&var_y+250 into line 1 of field "data"
drag from var_xprev, var_yprev to var_x+250, var_y+250
//wait until the mouseclick
put var_x+250 into var_xprev
put var_y+250 into var_yprev
//add one to var_x:
put var_x+1 into var_x
end repeat
choose browse tool
end mouseUp
You'll notice some variations to what we used above. First, notice that I moved the code to increase x by 1 to the bottom of the repeat loop. That just seemed a better place.
Second, notice lines 4-5 and line 7 in the repeat loop. They are set as comment lines now, so they do not get executed. But, they will if you delete the "//" in front of each. What would these do? Well, I added them to help me understand and troubleshoot the code. I do this all the time. After I perfect a script, I usually delete them, but I thought you might like to see them so as to learn a good programming trick to help you figure out what's going on in your script as you work on it. Line 7 - "wait until the mouseclick" - is a simple way to have the repeat loop pause at each loop and wait for you to click the mouse button. This lets you look at what is happening at each loop. Lines 4 and 5 put var_x and var_y into a (now hidden) card field titled "data." (This field can easily be made visible in the Application Browser tool.)
Let's move on graphing two more interesting curves -- the sine and cosine functions.
Graphing the Curves Derived from the Sine and Cosine Functions
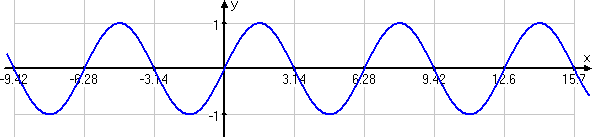
OK, let's explore the sine and cosine curves. First, here is a graph of the sine curve linked from purplemath.com:
It's important to understand how this curved shape is generated. For most people, the shapes, though familiar, are quite mysterious, even though everyone certainly graphed them at some point in high school. The explanation of these curves is rather simple and is derived by considering a circle.
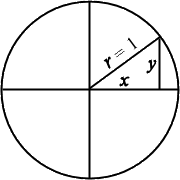
Here is a figure of the circle linked from the purplemath.com web site that will help explain things for us:
As you can see, the radius of this circle is conveniently set to 1. Any radius I draw will obviously intersect the circle at one and only one point. Now, take a moment and look at the figure above and estimate the angle that is formed at left point of the triangle formed by the line segments r and x. It looks to be about 30 degrees to me. Well, the sine of that angle is y and the cosine of that angle is x. That's it. It's no more complicated than that. So, the sine of an angle of 0 degrees would 0 and the cosine would be 1. The sine of an angle of 90 degrees would be 1 and cosine would be 0. What about 45 degrees? Although one might be first tempted to say both sine and cosine are .5 (half of 1), the answer is actually about .707. One way to reason this out is with the all-powerful Pythagorean Theorem, which for right triangles is a2 = b2 + c2 and is read as "a squared equals b squared plus c squared." b squared and c squared both equal .5, and the square root of .5 is .707 (when rounded to 3 decimal places).
Click here to try out a very nice interactive animation of the sine curve at intmath.com -- it nicely shows how the sine curve is formed just by tracing out the value of y.
Graphing the Sine and Cosine Functions in LiveCode
An important fact to remember throughout the next few minutes is that the maximum value of sine or cosine is 1 and the minimum value is 0. So, this is not a very large range for graphing purposes. So, obviously, we are going to need to multiply some value in our code to make the curve more readily apparent. So, tuck that thought away as we proceed to program these curves in LiveCode. We'll start with the sine curve.Fortunately, all need to do is revise a single line of code in the script for the parabola. And I'll bet you've already figured out which line of code I mean - line 3 of the final script shown above:
put -(var_x^2)/50 into var_y
LiveCode already includes the sine and cosine functions. These are "sin" and "cos," respectively. (Refer to the LiveCode dictionary to learn more about them.) To change from graphing a parabola to graphing the sine curve, it seems it should be as easy as change it first to the following:
put -(sin(var_x)) into var_y
But, not so fast. By default, LiveCode using radians instead of degrees to express an angle. (Rather than take the time to explain it here, I suggest you do a google search on the difference between radians and degrees. In short, radians are based on pi, not degrees, where 2*pi equals 360 degrees. Remember the formula for the circumference of a circle? "A=2*pi*r") We could stick with radians, but this would take some more programming gymnastics to get everything to work. So, we'll just convert radians to degrees by multiplying the value by (pi/180):
put -(sin(var_x * pi/180)) into var_y
Finally, we need to multiply everything by some number so the result will be bigger than 1. I think multiplying by 100 will do the trick. So, here is the final script:
put -(sin(var_x * pi/180))*100 into var_y
Let's start the graph as far left of the card as we can. Since the card is 500 pixels wide and high, let's set var_x to about -240. We'll repeat everything twice this amount, or 480 times. Here's what we get:
Let's duplicate this button and title it "Graph cosine function." We change the line of code above to the following:
I changed the brush color to blue. Here is the resulting graph:
So what?
I admit that the past three blog posts have been rather theoretical in nature. Being able to graph simple lines, parabolas, and the sine and cosine functions may impress our high school algebra teachers, but what good is all this for LiveCode development? In my next posting, I'll show an example that puts this graphing script to use in a blog posting that I'm thinking of calling "Lloyd's Math Fair Contest Entry."
A Mystery Remains
Although I'm tempted not to tell you this, there is one last mystery that, frankly, I've not been able to solve. Remember way back when (in my first blog posting in this graphing series) that we had to choose our first point "way out to the left" in order to avoid that awkward first line segment -- we chose -1000, -1000. Well, I'm actually wondering why we are not seeing the first line segment connecting -1000,-1000 with the first point of the parabola, sine curve, or cosine curve. I've played around a little bit with this. If you change this first point where the coordinates are both positive numbers - say 5, 5 - then that pesky line segment appears. So, it has something to do with the fact that the initial point is not shown on the visible area of the card. I hope anyone who knows more about this will help explain this for us.






No comments:
Post a Comment